概要
summary
In the previous tutorial, we successfully rendered a triangle in the center of our application window. We haven't paid much attention to the vertex positions that we have picked in our vertex buffer. In this tutorial, we will delve into the details of 3D positions and transformation. The outcome of this tutorial will be a 3D object rendered to screen. Whereas previous tutorials focused on rendering a 2D object onto a 3D world, here we show a 3D object.
前回のチュートリアルでは無事アプリケーション・ウインドウの中央に三角形を描画できました。我々は頂点バッファから取ってきた頂点の位置について余り気を払いませんでした。今回のチュートリアルでは三次元の位置と座標変換( トランスフォーム )を探求しましょう。このチュートリアルの成果は3Dのオブジェクトを画面に描画する事です。前回のチュートリアルでは3D空間に2Dオブジェクトをレンダリングする事に焦点を当てましたが、ここでは3Dオブジェクトを表示します。
3D空間
3D Spaces
In the previous tutorial, the vertices of the triangle were placed strategically to perfectly align themselves on the screen. However, this will not always be the case.
前回のチュートリアルでは、三角形の頂点は画面上に完全にそれ自身の位置で並ぶように図られて配置されました。しかし、こういったケースばかりではありません。
Thus, we need a system to denote objects in 3D space and a system to display them.
そこで物体を3D空間に示し、それを表示する座標系が必要となります。
In the real world, objects exist in 3D space.
現実の世界では、物体は3D空間に存在しています。
This means that to place an object in a particular position in the world, we would need to use a coordinate system and define three coordinates that correspond to the position.
これが意味する事は、物体を固有の位置で世界に表示するには、座標を使い、位置に対応する3つの座標を定義する必要があるという事です。
In computer graphics, 3D spaces are most commonly in Cartesian coordinate system. In this coordinate system, three axes, X, Y, and Z, perpendicular to each other, dictate the coordinate that each point in the space has.
コンピューターグラフィクスでは3D空間は一般にデカルト座標系を使って表します。この座標系はX,Y,Zの3軸が互いに直交して、空間にあるそれぞれの点を座標に取ります。
This coordinate system is further divided into left-handed and right-handed systems.
この座標系はさらに左手系と右手系に分かれています。
In a left-handed system, when X axis points to the right and Y axis points to up, Z axis points forward. In a right-handed system, with the same X and Y axes, Z axis points backward.
左手系では、X軸が右を指し、Y軸が上を指せばZ軸は奥を指します。右手系では、XとY軸が同様ならば、Z軸が手前を指します。
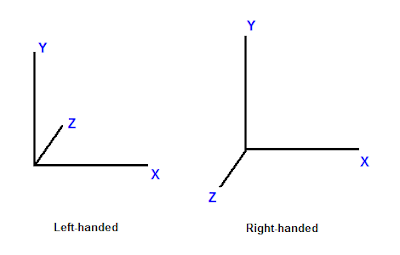 |
| 図1.座標系の違い |
Now that we have talked about the coordinate system, consider 3D spaces.
これで座標系について説明出来たので、3D空間を考えましょう。
A point has different coordinates in different spaces.
一つの点は色々な空間の座標を持ちます。
As an example in 1D, suppose we have a ruler and we note the point, P, at the 5-inch mark of the ruler.
1Dの例として、定規の5インチの場所に点Pがあるとしましょう。
Now, if we move the ruler 1 inch to the right, the same point lies on the 4-inch mark.
ここでもし定規を1インチ右へ動かすと、同じ点は4インチのマークの場所にのります。
By moving the ruler, the frame of reference has changed.
定規を動かすことによって、基準となるマスが変わったのです。
Therefore, while the point hasn't moved, it has a new coordinate.
そのため、この点は動いていませんが新しい座標を持つことになります。
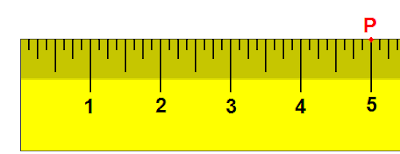 |
| 図2.1Dで表した空間 |
In 3D, a space is typically defined by an origin and three unique axes from the origin: X, Y and Z. There are several spaces commonly used in computer graphics: object space, world space, view space, projection space, and screen space.
3Dでは、空間は一般的に原点とそこから伸びる固有の軸(X、Y、Z)で定義されます。
CGで使われる座標空間系の種類は複数あります。:オブジェクト空間、ワールド空間、ビュー空間、プロジェクション空間、そしてスクリーン空間です。
オブジェクト空間
Object Space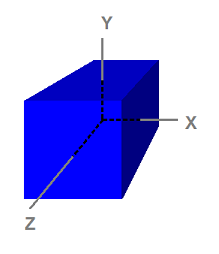 |
| 図3.オブジェクト空間に定義された立方体 |
Notice that the cube is centered on the origin.
この立方体は原点を中心に持つ事に注目して下さい。
Object space, also called model space, refers to the space used by artists when they create the 3D models.
オブジェクト空間はモデルスペースとも呼ばれ、デザイナーが3Dモデルを作る時に使われます。
Usually, artists create models that are centered around the origin so that it is easier to perform transformations such as rotations to the models, as we will see when we discuss transformation.
通常、デザイナーは回転などのモデルへ適用する座標変換を簡単に実行するために、原点を心にしてモデルを作ります。これは座標変換を後で説明した時に理解できるでしょう。
The 8 vertices have the following coordinates
立方体の8つの頂点は以下の座標を持ちます。
(-1, 1, -1)
( 1, 1, -1)
(-1, -1, -1)
( 1, -1, -1)
(-1, 1, 1)
( 1, 1, 1)
(-1, -1, 1)
( 1, -1, 1)
Because object space is what artists typically use when they design and create models, the models that are stored on disk are also in object space.
オブジェクト空間はデザイナーがモデルのデザインと作成をする時に使う典型的な座標系なのでディスク上に保管されているモデルのデータもオブジェクトスペースにあると言えます。
An application can create a vertex buffer to represent such a model and initialize the buffer with the model data. Therefore, the vertices in the vertex buffer will usually be in object space as well.
アプリケーションは頂点バッファをこの様なモデルを表現するために作り、そのバッファをモデルデータとして初期化出来ます。そのため、頂点バッファの頂点も通常はオブジェクト空間の座標系になります。
This also means that the vertex shader receives input vertex data in object space.
これは頂点シェーダーが入力頂点データをオブジェクト座標として受け取る事も意味します。
ワールド空間
World SpaceWorld space is a space shared by every object in the scene.
ワールド空間はシーンを構成する全てのオブジェクトによって共有される空間です。
It is used to define spatial relationship between objects that we wish to render.
それは描画するオブジェクト間に特別の関係を定義したい時に使われます。
To visualize world space, we could imagine that we are standing in the south-western corner of a rectangular room facing north.
ワールド空間を視覚化するには、矩形の部屋の南西の角に北に向かって立っている状態を想像して下さい。
We define the corner that our feet are standing at to be the origin, (0, 0, 0).
我々が立っている角を原点(0, 0, 0)と定義します。
The X axis goes to our right; the Y axis goes up; and the Z axis goes forward, the same direction as we are facing.
その位置から:X軸は右へ:Y軸は上へ:Z軸は我々の向きと同じで前方へ伸びます。
When we do this, every position in the room can be identified with a set of XYZ coordinates.
このように定義すると、部屋の中の全ての位置がXYZ座標の組み合わせで表すことが出来ます。
For instance, there may be a chair 5 feet in front and 2 feet to the right of us.
例えば我々の5フィート前、2フィート右に椅子があるかも知れません。
There may be a light on the 8-foot-high ceiling directly on top of the chair.
その椅子の上、8フィートの高さには天井があり、そこにライトがあるかも知れません。
We can then refer to the position of the chair as (2, 0, 5) and the position of the light as (2, 8, 5).
その場合、椅子の位置は (2, 0, 5)で、ライトの位置は (2, 8, 5)で表せます。
As we see, world space is so-called because they tell us where objects are in relation to each other in the world.
この様に、ワールド空間は世界におけるオブジェクト同士の位置関係を教えてくれるのでその様な名前が付いています。
ビュー空間
View SpaceView space, sometimes called camera space, is similar to world space in that it is typically used for the entire scene.
ビュース空間(カメラスペースとも呼ばれます)は通常、シーン全体のために使われるという点でワールドスペースと似ています。
However, in view space, the origin is at the viewer or camera.
ただしビュースペースでは原点がビューアー(見ている人)かカメラとなります。
The view direction (where the viewer is looking) defines the positive Z axis.
視野の方向(ビューアーが見ている方向)によってZ軸の正の向きを定義します。
An "up" direction defined by the application becomes the positive Y axis as shown below.
アプリケーションによって定義される上方向は以下に示すようにY軸の正の方向になります。
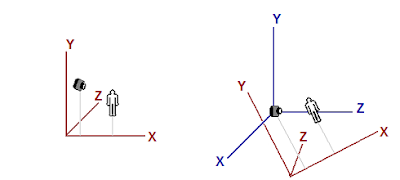 |
| 同じオブジェクトがワールドスペース(左)とビュースペース(右)にある図 |
The left image shows a scene that consists of a human-like object and a viewer (camera) looking at the object.
左の図は人間の様なオブジェクトとそれを見ているビューアー(カメラ)から構成されるシーンを示しています。
The origin and axes that are used by world space are shown in red.
ワールドスペースで使われる原点と軸は赤で示しています。
The right image shows the view space in relation to world space.
右側の図はビュースペースをワールドスペースとの関連で示しています。
The view space axes are shown in blue.
ビュースペースの軸は青で示されています。
For clearer illustration, the view space does not have the same orientation as the world space in the left image to readers.
分かり易く図解するために、読み手にとって、ビュースペースの向きは左の図のワールドスペースと同じにはしていません。
Note that in view space, the viewer is looking in the Z direction.
ビュースペースではビューアーはZ軸を向いている事に注意して下さい。
(訳注:ビュー空間のまとめ
ビュー空間はビューア(カメラや人の目)を原点にして、その視線の方向をZ軸の+方向としてオブジェクトを再配置した座標空間です。ビュー座標系と言った方がしっくり来るかも知れません。)
プロジェクション空間
Projection SpaceProjection space refers to the space after applying projection transformation from view space.
プロジェクションスペース(射影空間)とはビュースペースから プロジェクショントランスフォームを適用した後の空間の事を言います。(訳注:これに関しての詳細は下の方にある座標変換のセクションにあります。)
In this space, visible content has X and Y coordinates ranging from -1 to 1, and Z coordinate ranging from 0 to 1.
この空間では見える物は-1から1の範囲にXとYの座標を持ち、Z座標は0から1の範囲となります。
スクリーンスペース
Screen SpaceScreen space is often used to refer to locations in the frame buffer.
スクリーン空間はしばしばフレームバッファの位置を参照するのに使わます。 (訳注:フレームバッファというのはそのフレーム(描画時間単位)で最終的に出力される画面情報を収めたメモリ領域です。)
Because frame buffer is usually a 2D texture, screen space is a 2D space.
フレームバッファは通常2Dテクスチャなので、スクリーン空間は2D空間です。
The top-left corner is the origin with coordinates (0, 0). The positive X goes to right and positive Y goes down.
左上の端の座標が原点(0, 0)となります。正方向のXは右へ、正方向のYは下へ伸びます。
For a buffer that is w pixels wide and h pixels high, the most lower-right pixel has the coordinates (w - 1, h - 1).
幅wピクセルと高さhピクセルのバッファの場合、一番右下のピクセルの座標は(w -1, h -1)となります。
空間から空間への座標変換
Space-to-space Transformation
Transformation is most commonly used to convert vertices from one space to another.
座標変換は通常、頂点をある空間から別の空間へ変換するために使われます。
In 3D computer graphics, there are logically three such transformations in the pipeline: world, view, and projection transformation.
3DCGでは理論上、パイプライン中に次のような座標変換が存在します。:ワールド、ビュー、そしてプロジェクション変換です。
Individual transformation operations such as translation, rotation, and scaling are covered in the next tutorial.
平行移動、回転、拡大縮小等の個々の変換処理は次のチュートリアルで説明します。
ワールド変換
World TransformationWorld transformation, as the name suggests, converts vertices from object space to world space.
ワールド変換は名前が示す通り、頂点をオブジェクト空間からワールド空間へ変換します。
It usually consists of one or more scaling, rotation, and translation, based on the size, orientation, and position we would like to give to the object.
我々はオブジェクトに対してサイズや向きや位置を変更したい事があるでしょう。ワールド変換は 通常 、それらを可能にする様な、1つかそれ以上の 拡大、回転、平行移動 と言った操作の組み合わせで構成されます。
Every object in the scene has its own world transformation matrix. This is because each object has its own size, orientation, and position.
シーン中の全てのオブジェクトが独自のワールド変換行列を持ちます。なぜならそれぞれのオブジェクトが独自の大きさ、向き、そして位置を持つからです。
(訳注:厳密に言えば、個々のオブジェクトはオブジェクト空間で定義された向きと大きさをそのまま出力すれば良い場合もあるかも知れません。しかし位置がそのままだと、シーンを構成する全てのオブジェクトが同じ場所(ワールドスペースの原点)に表示されてしまうので位置のためにだけでも個々のオブジェクトに対するワールド変換が必要だったりします。)
ビュー変換
View TransformationAfter vertices are converted to world space, view transformation converts those vertices from world space to view space.
頂点がワールド空間に変換された後、ビュー変換がこれらの頂点をワールド空間からビュー空間へ変換します。
Recall from earlier discussion that view space is what the world appears from the viewer's (or camera's) perspective.
ビュー空間はビューアー(またはカメラ)から見た視野の世界として表されるという先の説明を思い出して下さい。
In view space, the viewer is located at origin looking out along the positive Z axis.
ビュー空間では、ビューアーは原点にZ軸の正の方向を向いて配置されます。
It is worth noting that although view space is the world from the viewer's frame of reference, view transformation matrix is applied to vertices, not the viewer.
ビュース空間はビューアーの座標系から見た世界であるにも関わらず、ビュー変換行列を適用するのはビューアーではなく、頂点全般だという事に注意する必要があります。
Therefore, the view matrix must perform the opposite transformation that we apply to our viewer or camera.
そういう訳でビュー行列は、ビューアーやカメラに適用するものとは逆の座標変換を実行する必要があります。
For example, if we want to move the camera 5 units towards the -Z direction, we would need to compute a view matrix that translates vertices for 5 units along the +Z direction.
例えばカメラをマイナスZ方向に5単位移動させるなら、頂点をプラスZ方向に沿って5単位平行移動させる様な ビュー行列を計算する必要があります。
Although the camera has moved backward, the vertices, from the camera's point of view, have moved forward.
そのカメラは後ろに動きますが、頂点はカメラの視点から見て前方へ動きます。
In XNA Math a convenient API call XMMatrixLookAtLH() is often used to compute a view matrix.
XNA Math の便利なAPI呼び出しのXMMatrixLookAtLH()が、しばしばビュー行列の計算に使われます。(訳注:他の行列関数一覧)
We would simply need to tell it where the viewer is, where it's looking at, and the direction representing the viewer's top, also called the up-vector, to obtain a corresponding view matrix.
それを使って対応するビュー行列を得るには、単にビューアーがどこにあり、どこを見ていて、どの方向がビューアーの上(アップベクトルとも呼ばれる)なのかを教えれば良いです。
プロジェクション変換
Projection TransformationProjection transformation converts vertices from 3D spaces such as world and view spaces to projection space.
プロジェクショントランスフォーム(射影変換)はワールドスペースやビュースペースといった3D空間から、頂点をプロジェクションスペースへ変換します。
(訳注:Direct3D9の頃の説明も参考になります。)
In projection space, X and Y coordinates of a vertex are obtained from the X/Z and Y/Z ratios of this vertex in 3D space.
プロジェクションスペースでは、頂点のXとY座標は3D空間における頂点の X/Z と Y/Zという比から得られます。
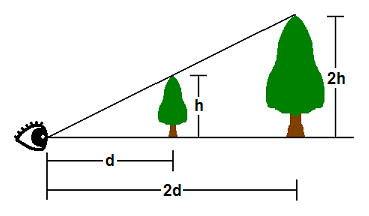 |
| 図5.プロジェクション |
In 3D space, things appear in perspective. That is, the closer an object is, the larger it appears.
3D空間中の物体は遠近法で表示されます。つまり近いもの程、大きく表示されるという分けです。
As shown, the tip of a tree that is h units tall at d units away from the viewer's eye will appear at the same point as the tip of another tree 2h units tall and 2d units away.
図の様に、 ビューアーの目からd離れた所にある 高さhの木の頂上は 、2d離れた所にある高さ2hの木と同じ位置に見えます。
Therefore, where a vertex appears on a 2D screen is directly related to its X/Z and Y/Z ratios.
そういう訳で、2D画面状の何処に頂点が現れるかは、X/ZとY/Zの比と直接関連付けられます。
(訳注:ここから視野の説明がしばらく続きます。)
One of the parameters that defines a 3D space is called the field-of-view (FOV).
3D空間を定義するパラメーターの一つに視野(FOV)と呼ばれるものがあります。
FOV denotes which objects are visible from a particular position, while looking in a particular direction.
視野は特定の位置、向きの時にどのオブジェクトが見えるかを表します。
Humans have a FOV that is forward-looking (we can't see what is behind us), and we can't see objects that are too close or too far away.
人間が持つ視野は次のような特性があります。
・前向き(我々は自分の後ろにある物が見えません)
・近すぎる物や遠すぎる物は見えない。
In computer graphics, the FOV is contained in a view frustum.
コンピューターグラフィクスでは、視野は視錘台(図6)に含まれます。
(訳注:ここから視錐台の説明がしばらく続きます。)
The view frustum is defined by 6 planes in 3D.
視錐台は3次元上の6平面で定義されます。
Two of these planes are parallel to the XY plane. These are called the near-Z and far-Z planes.
これらの平面の内の2つは、XY平面に平行です。これを近-Z 平面と 遠-Z 平面と呼びます。
(訳注:XY平面とは、ここでは奥行きを伴わない2D平面の事です。近、遠Z平面はクリップ平面と呼ばれたりもします。)
The other four planes are defined by the viewer's horizontal and vertical field of view.
他の4つの平面はビューアーの水平視野と垂直視野によって定義されます。
The wider the FOV is, the wider the frustum volume is, and the more objects the viewer sees.
視野が広ければ視錐台も広い事を意味し、ビューアーからはより沢山の物が見えます。
The GPU filters out objects that are outside the view frustum so that it does not have to spend time rendering something that will not be displayed. This process is called clipping.
GPUはディスプレイに表示される事のない部分まで描画して時間を消耗す分けにはいかないので、視錐台の外のオブジェクトクトを除去します。このプロセスはクリッピングと呼ばれます。
The view frustum is a 4-sided pyramid with its top cut off.
視錐台は頂上が切り取られた四角錐です。
Clipping against this volume is complicated because to clip against one view frustum plane, the GPU must compare every vertex to the plane's equation.
この立体に対してクリッピングを行うのは複雑です。なぜなら視錐台の一つの平面に対してクリッピングを行う毎に、GPUはすべての頂点と平面の方程式で(領域内かどうかを)比較する必要があるからです。
Instead, the GPU generally performs projection transformation first, and then clips against the view frustum volume.
替りに、一般的にGPUは始めにプロジェクション変換を実行し、そして次に視錐台に対してクリッピングを行います。
(訳注:ここでクリッピングという概念を軸にして視錐台の話題がプロジェクション変換という元の話題と繋がりました。)
The effect of projection transformation on the view frustum is that the pyramid shaped view frustum becomes a box in projection space.
視錐台に対するプロジェクション変換の効果は、角錐型の視錐台がプロジェクション空間においては箱型になる事です。
This is because, as mentioned previously, in projection space the X and Y coordinates are based on the X/Z and Y/Z in 3D space.
なぜなら前に述べたように、プロジェクション空間のXとY座標は3D空間のX/ZとY/Zを元にするからです。
Therefore, point a and point b will have the same X and Y coordinates in projection space, which is why the view frustum becomes a box.
ですから、(下の図の)点aと点bはプロジェクション空間において同じXとYの座標が当てられます。これが視錐台が箱型になる理由です。
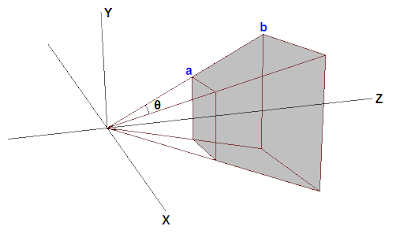 |
| 図6.視錐台 |
Suppose that the tips of the two trees lie exactly on the top view frustum edge.
2本の木の頂上が視錐台の上辺に正確に沿っていると仮定して下さい。
Further suppose that d = 2h.
そしてd= 2hとしましょう。
(訳注:図5参照。木までの距離をdで表し、木の高さをhで表しています。また、木の高さはその距離における視錐台の高さと一緒です。)
The Y coordinate along the top edge in projection space will then be 0.5 (because h/d = 0.5).
その場合プロジェクションスペースでは、上辺に沿ったY座標は0.5となります(なぜなら h/d = 0.5) 。
(訳注:上の方にあった図5の解説でXとYの値がX/ZとY/Zによって決まった事を思い出して下さい。 つまり簡単に言えばプロジェクション空間までの高さ= 3D空間での高さ / Z(=距離) です。)
Therefore, any Y values post-projection that are greater than 0.5 will be clipped by the GPU.
従って投射された0.5以上のYの値はGPUによってカットされます。
The problem here is that 0.5 is determined by the vertical field of view chosen by the program, and different FOV values result in different values that the GPU has to clip against.
ここで問題なのは、この0.5という値はプログラムによって選ばれた垂直視野によって決まるものであり、視野が異なればGPUがクリップしなければならない値も違ったものになるという事です。
To make the process more convenient, 3D programs generally scale the projected X and Y values of vertices so that the visible X and Y values range from -1 to 1.
このプロセスをもっと便利にするために、3Dプログラムは一般に、表示されるXとYの範囲が-1~1となるように、射影された頂点のxとyの値を、スケーリングします。
In other words, anything with X or Y coordinate that's outside the [-1 1] range will be clipped out.
つまり、[-1 1]の範囲外の全てのxまたはy座標はカットされる事になります。
To make this clipping scheme work, the projection matrix must scale the X and Y coordinates of projected vertices by the inverse of h/d, or d/h.
このクリッピングのメカニズムを機能させるために射影行列は、 射影された頂点のXとY座標を h/dの逆、すなわちd/hによってスケーリングする必要があります。(訳注:ここでのd/hのhはオブジェクトの高さではなく、オブジェクトの位置の視錐台の上辺の高さを指していると思われます。)
d/h is also the cotangent of half of FOV.
d/hは視野の半分のコタンジェントでもあります。
With scaling, the top of the view frustum becomes h/d * d/h = 1.
スケーリングによって、視錐台の頂上はh/d*d/h=1となります。
(訳注:確かにh/d*d/hという式で使われる2つのhが両方とも同じ(視錐台の上辺の高さ)なら、この式の結果は1になる分けです。しかしこれはカットの基準となる高さを表しているのであり、実際計算されるのはh/d*d/hという式の左側のhがオブジェクトの高さを、右側のhが視錐台上辺の高さを指すのだと思われます。)
Anything greater than 1 will be clipped by the GPU. This is what we want.
1より大きい物は全てGPUによってカットされます。これは我々が欲しかった挙動です。
A similar tweak is generally done for the Z coordinate in projection space as well.
同様の調整は一般にプロジェクション空間のZ座標でも行われます。
We would like the near and far Z planes to be at 0 and 1 in projection space, respectively.
我々はプロジェクション空間の近Z平面を0に、遠Z平面を1にしたいのです。
When Z = near-Z value in 3D space, Z should be 0 in projection space; when Z = far-Z in 3D space, Z should be 1 in projection space.
Z = 3D空間上の近-Z平面 の場合はプロジェクション空間においては0になり、 Z = 3D空間上の遠-Z平面 の場合はプロジェクション空間では1になるべきです。
After this is done, any Z values outside [0 1] will be clipped out by the GPU.
それがなされた後は、[0 1]の範囲外のZ値は全て、GPUによってクリッピングされる事となります。
In Direct3D 11, the easiest way to obtain a projection matrix is to call the XMMatrixPerspectiveFovLH() method.
Direct3D11では、射影行列を得る一番簡単な方法は、XMMatrixPerspectiveFovLH()関数を呼ぶ事です。
We simply supply 4 parametersーFOVy, Aspect, Zn, and Zfーand get back a matrix that does everything necessary as mentioned above.
我々は単に4つの引数-FovAngleY, AspectHByW, NearZ,そしてFarZを供給すれば上で述べた必要な事を全てやってくれる行列が手に入ります。
(訳注:引数名がDirect3D10のチュートリアルで使われていた関数D3DXMatrixPerspectiveFovLHの引数名のままだったので修正しました)
FOVy is the field of view in Y direction. Aspect is the aspect ratio, which is ratio of view space width to height.
FOVAngleYはY方向の視野です。AspectHPyWはアスペクト比であり、ビュー空間の幅と高さの比です。
From FOVy and Aspect, FOVx can be computed.
FOVAngleXは FOVAngleY と AspectHPyW から 計算できます。
This aspect ratio is usually obtained from the ratio of the render target width to height.
このアスペクト比は通常、描画ターゲットの幅と高さの比から得ることが出来ます。
Zn and Zf are the near and far Z values in view space, respectively.
NearZとFarZ はそれぞれビュー空間における近-Z平面と遠-Z平面の値です。(訳注:つまり視野の近距離の限界と遠距離の限界です。)
座標変換行列を使う
Using Transformation
In the previous tutorial, we wrote a program that renders a single triangle to screen.
前のチュートリアルでは画面に一つの三角形を描画するプログラムを書きました。
When we create the vertex buffer, the vertex positions that we use are directly in projection space so that we don't have to perform any transformation.
その際に頂点バッファを作った時、使用した頂点の位置はプロジェクション空間にそのまま存在したと言えるので何の座標変換も実行する必要がありませんでした。
Now that we have an understanding of 3D space and transformation, we are going to modify the program so that the vertex buffer is defined in object space, as it should be.
我々は3D空間と座標変換の知識を得たので、頂点バッファがオブジェクト空間中に適切に定義されるようにプログラムを改造しましょう。
Then, we will modify our vertex shader to transform the vertices from object space to projection space.
次に頂点をオブジェクト空間からプロジェクション空間へ変換するように頂点シェーダーを改造しましょう。
頂点バッファの改造
Modifying the Vertex BufferSince we started representing things in three dimensions, we have changed the flat triangle from the previous tutorial to a cube.
我々は3次元空間上の物体を表現し始めたので、描画対象を前回のチュートリアルの平面の三角形から立方体に変えました。
This will allow us to demonstrate these concepts much clearer.
これにより、一連の概念がより明確に説明できるようになるでしょう。
SimpleVertex vertices[] =
{
{ XMFLOAT3( -1.0f, 1.0f, -1.0f ), XMFLOAT4( 0.0f, 0.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, 1.0f, -1.0f ), XMFLOAT4( 0.0f, 1.0f, 0.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, 1.0f, 1.0f ), XMFLOAT4( 0.0f, 1.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( -1.0f, 1.0f, 1.0f ), XMFLOAT4( 1.0f, 0.0f, 0.0f, 1.0f ) },
{ XMFLOAT3( -1.0f, -1.0f, -1.0f ), XMFLOAT4( 1.0f, 0.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, -1.0f, -1.0f ), XMFLOAT4( 1.0f, 1.0f, 0.0f, 1.0f ) },
{ XMFLOAT3( 1.0f, -1.0f, 1.0f ), XMFLOAT4( 1.0f, 1.0f, 1.0f, 1.0f ) },
{ XMFLOAT3( -1.0f, -1.0f, 1.0f ), XMFLOAT4( 0.0f, 0.0f, 0.0f, 1.0f ) },
};
If you notice, all we did was specify the eight points on the cube, but we didn't actually describe the individual triangles.
お気付きかも知れませんが、ここでは立方体の8つの頂点を指定しただけであり、これでは個々の三角形を構成した事にはなりません。(訳注:XMFLOAT3が頂点の位置、XMFLOAT4が頂点の色です。)
If we passed this in as-is, the output would not be what we expect.
もしこれを中へそのまま通せば、出力は我々が予期したものにはならないでしょう。
We will need to specify the triangles that form the cube through these eight points.
我々は立方体を構成するこれら8つの点から三角形を指定する必要があります。
On a cube, many triangles will be sharing the same vertex and it would be a waste of space to redefine the same points over and over again.
立方体では多くの三角形が同じ頂点を共有します。同じ点を何度も再定義すると、メモリ空間の浪費になります。
As such, there is a method to specify just the eight points, and then let Direct3D know which points to pick for a triangle.
そのため、単に8つの頂点を指定し、そしてDirect3Dにそこからどの点を三角形のために選ぶかを教える…という方法があります。
This is done through an index buffer.
これはインデックスバッファを通して成されます。
(訳注:チュートリアル2でも頂点情報を節約する方法としてトライアングルストリップを扱いましたが、ここで説明されるインデックスバッファはこれとはまた別の方法です。)
An index buffer will contain a list, which will refer to the index of vertices in the buffer, to specify which points to use in each triangle.
インデックスバッファはバッファ中のどの頂点がどの三角形の中で使われるかを特定するためのリストです。
The code below shows which points make up each of our triangles.
以下のコードはどの点がどの三角形を構成するかを示します。
// インデックスバッファの作成
WORD indices[] =
{
3,1,0,
2,1,3,
0,5,4,
1,5,0,
3,4,7,
0,4,3,
1,6,5,
2,6,1,
2,7,6,
3,7,2,
6,4,5,
7,4,6,
};
As you can see, the first triangle is defined by points 3, 1, and 0.
ご覧のように、最初の三角形は点、3,1,0で定義されています。
This means that the first triangle has vertices at: ( -1.0f, 1.0f, 1.0f ),( 1.0f, 1.0f, -1.0f ), and ( -1.0f, 1.0f, -1.0f ), respectively.
これは最初の三角形が持つ頂点はそれぞれ ( -1.0f, 1.0f, 1.0f ),( 1.0f, 1.0f, -1.0f ), ( -1.0f, 1.0f, -1.0f ) だという事を意味します。
(訳注:インデクスバッファ WORD indices[]の中身は、 チュートリアル中の例としてその一つ上で定義した SimpleVertex vertices[]の配列の番号(インデクス)に対応してます。配列の番号は0から始まる事に注意して見比べて下さい。)
There are six faces on the cube, and each face is comprised of two triangles. Thus, you see 12 total triangles defined here.
立方体には6つの面があり、それぞれの面は2つの三角形から構成されます。そういう分けでここには合計12の三角形が定義されています。
Since each vertex is explicitly listed, and no two triangles are sharing edges (at least, in the way it has been defined), this is considered a triangle list.
それぞれの頂点は明確に並べられて、そして2つの三角形が辺を共有している訳でもありません(少なくともこの方法ではそう定義しました。)。なのでこれはトライアングルリストだと考えられます。
In total, for 12 triangles in a triangle list, we will require a total of 36 vertices.
合計では、トライアングルリストの中の12の三角形のために、合計36個の頂点が必要になります。(訳注:インデックスバッファのインデックスが36必要だという事を意味します。)
The creation of the index buffer is very similar to the vertex buffer, where we specified parameters such as size and type in a structure, and called CreateBuffer.
インデクッスバッファの作成は頂点バッファと良く似ています。構造体でサイズや型等の引数をこしらえてCreateBufferを呼びます。
(訳注:頂点バッファもインデックスバッファも型名はID3D11Bufferであり、どちらもCreateBufferを使って作成するのですね。)
The type is D3D11_BIND_INDEX_BUFFER, and since we declared our array using DWORD, we will use sizeof(DWORD).
タイプは D3D11_BIND_INDEX_BUFFERであり、DWORDを使って配列を宣言したのでsizeof(DWORD)を使います。
(訳注:タイプとはCreateBuffer()の引数にセットする構造体 D3D11_BUFFER_DESC のメンバのBindFlagsの事を指しています。このメンバはバッファの使われ方を指定します。ここではインデックスバッファとして使うのでD3D11_BIND_INDEX_BUFFERを指定します。)
D3D11_BUFFER_DESC bd;
ZeroMemory( &bd, sizeof(bd) );
bd.Usage = D3D11_USAGE_DEFAULT;
bd.ByteWidth = sizeof( WORD ) * 36; // 36 vertices needed for 12 triangles in a triangle list
bd.BindFlags = D3D11_BIND_INDEX_BUFFER;
bd.CPUAccessFlags = 0;
bd.MiscFlags = 0;
InitData.pSysMem = indices;
if( FAILED( g_pd3dDevice->CreateBuffer( &bd, &InitData, &g_pIndexBuffer ) ) )
return FALSE;
Once we created this buffer, we will need to set it so that Direct3D knows to refer to this index buffer when generating the triangles.
このバッファを作った後は、Direct3Dが三角形を製造する時にインデックスバッファを参照するのだと分かるようにセットする必要があります。
We specify the pointer to the buffer, the format, and the offset in the buffer to start referencing from.
それにはバッファへのポインター、フォーマット、そしてレンダリングを始めるバッファへがどこから開始するのかオフセットを指定します。
(訳注:オフセットというのはメモリを扱うプログラムでしばしば登場する概念です。バッファ(メモリ配列)の中には、今回描画するためのデータ意外にもデータを含める事も出来ます。オフセットは、そういったメモリ配列の中から任意のデータを指定するという意味で配列のインデックスのようなものです。何バイトデータを読み飛ばすかとう形でオフセットを指定します。今回の様にバッファ=目的のデータだけ、という場合は0を指定します。)
// インデックスバッファのセット
g_pImmediateContext->IASetIndexBuffer( g_pIndexBuffer, DXGI_FORMAT_R16_UINT, 0 );
頂点シェーダの改造
Modifying the Vertex ShaderIn our vertex shader from the previous tutorial, we take the input vertex position and output the same position without any modification.
前回のチュートリアルの頂点シェーダでは頂点位置を入力として受け取り、何の変更も加えずに同じ位置を出力しました。
We can do this because the input vertex position is already defined in projection space.
これが可能なのは、入力された頂点位置が既にプロジェクション空間にあるものとして定義された場合です。
Now, because the input vertex position is defined in object space, we must transform it before outputting from the vertex shader.
今回の入力頂点はオブジェクト空間として定義したので、頂点シェーダから出力する前に座標変換をする必要があります。
We do this with three steps: transform from object to world space, transform from world to view space, and transform from view to projection space.
これは3つのステップで行います。:
オブジェクト空間からワールド空間への変換、
ワールド空間からビュー空間への変換、そして
ビュー空間からプロジェクション空間への変換です。
The first thing that we need to do is declare three constant buffer variables.
我々が初めにする必要があるのは3つの定数バッファ変数の宣言です。
Constant buffers are used to store data that the application needs to pass to shaders.
定数バッファはアプリケーションがシェーダーへ渡すのに必要なデータを格納するのに使われます。
Before rendering, the application usually writes important data to constant buffers, and then during rendering the data can be read from within the shaders.
描画の前、アプリケーションは通常、重要なデータを定数バッファに書き込みます。書き込まれた定数バッファは描画中にシェーダー内から読む事が出来ます。
In an FX file, constant buffer variables are declared like global variables in a C++ struct.
FXファイル(エフェクトファイル)では定数バッファ変数はC++のグローバル変数の構造体の様に宣言されます。
The three variables that we will use are the world, view, and projection transformation matrices of the HLSL type "matrix."
我々が使う3つの変数はHLSLの”matrix”型に属するワールド、ビュー、プロジェクション変換行列です。
Once we have declared the matrices that we will need, we update our vertex shader to transform the input position by using the matrices.
必要となる行列の宣言が済んだら頂点シェーダーを更新します。 その行列を使って入力された位置情報を変換するために、
A vector is transformed by multiplying the vector by a matrix.
ベクトルは行列を掛けることによって座標変換されます。
In HLSL, this is done using the mul() intrinsic function. Our variable declaration and new vertex shader are shown below:
HLSLでこれをするにはHLSLに元から用意されているmul()という関数を使います。
我々の変数宣言と新しい頂点シェーダーは下の通りです。
cbuffer ConstantBuffer : register( b0 )
{
matrix World;
matrix View;
matrix Projection;
}
//
// Vertex Shader
//
VS_OUTPUT VS( float4 Pos : POSITION, float4 Color : COLOR )
{
VS_OUTPUT output = (VS_OUTPUT)0;
output.Pos = mul( Pos, World );
output.Pos = mul( output.Pos, View );
output.Pos = mul( output.Pos, Projection );
output.Color = Color;
return output;
}
In the vertex shader, each mul() applies one transformation to the input position.
頂点シェーダーでは、 入力された位置に対してそれぞれのmul()が一つの座標変換を加えます。
The world, view, and projection transformations are applied in that order sequentially.
ワールド、ビュー、プロジェクション変換はその命令された順番通りにに適用されます。
This is necessary because vector and matrix multiplication is not commutative.
ベクトルと行列は可換性がないので、この事は避ける事が出来ません。
(訳注:可換性=交換法則です。a・b = b・a なら交換法則を満たします。これがないという事は、演算の順番によって結果が変わるという事を意味します。)
行列のセットアップ
Setting up the MatricesWe have updated our vertex shader to transform using matrices, but we also need to define three matrices in our program.
頂点シェーダが行列を使って座標変換を実行するように更新をしましたが、依然としてプログラム中に3つの行列を定義する必要があります。
These three matrices will store the transformation to be used when we render.
それら3つの行列がレンダリングを行う時に使われる座標変換を格納します。
Before rendering, we copy the values of these matrices to the shader constant buffer.
レンダリングをする前、我々はこれらの行列の値をシェーダーの定数バッファにコピーします。
Then, when we initiate the rendering by calling Draw(), our vertex shader reads the matrices stored in the constant buffer.
Draw()を呼んで描画を開始する時、頂点シェーダーは定数バッファに格納された行列を読みます。
In addition to the matrices, we also need an ID3D11Buffer object that represents the constant buffer.
行列に加え、我々はID3D11Bufferオブジェクトが必要です。これが定数バッファを表します。
Therefore, our global variables will have the following addition:
そういう分けで、グローバル変数に以下の追加をしましょう。
ID3D11Buffer* g_pConstantBuffer = NULL;
XMMATRIX g_World;
XMMATRIX g_View;
XMMATRIX g_Projection;
To create the ID3D11Buffer object, we use ID3D11Device::CreateBuffer() and specify D3D11_BIND_CONSTANT_BUFFER.
ID3D11Bufferオブジェクトを作るにはID3D11Device::CreateBuffer()を使い、D3D11_BIND_CONSTANT_BUFFERを指定します。
(訳注:頂点バッファやインデックスバッファと同様、定数バッファも ID3D11Bufferと D3D11_BUFFER_DESC構造体を用意してからCreateBuffer()します。)
D3D11_BUFFER_DESC bd;
ZeroMemory( &bd, sizeof(bd) );
bd.Usage = D3D11_USAGE_DEFAULT;
bd.ByteWidth = sizeof(ConstantBuffer);
bd.BindFlags = D3D11_BIND_CONSTANT_BUFFER;
bd.CPUAccessFlags = 0;
if( FAILED(g_pd3dDevice->CreateBuffer( &bd, NULL, &g_pConstantBuffer ) ) )
return hr;
The next thing that we need to do is come up with three matrices that we will use to do the transformation.
次にする必要がある事は座標変換に使う行列を用意する事です。
We want the triangle to be sitting on origin, parallel to the XY plane.
我々は三角形をXY平面に平行に、原点を中心にしてセットしたいのです。
This is exactly how it is stored in the vertex buffer in object space.
これはオブジェクト空間の頂点バッファがどう格納されたかという事と正確に一致します。
Therefore, the world transformation needs to do nothing, and we initialize the world matrix to an identity matrix.
従って、ワールド変換は何もする必要がなく、ワールド行列は単位行列として初期化します。
We would like to set up our camera so that it is situated at [0 1 -5], looking at the point [0 1 0].
カメラは[0 1 -5]の位置に、[0 1 0]の位置を向くようにセットアップする事にしましょう。
We can call XMMatrixLookAtLH() to conveniently compute a view matrix for us using the up vector [0 1 0] since we would like the +Y direction to always stay at top.
便利なことに、XMMatrixLookAtLH()を呼べばビュー行列を計算できます。我々は+y方向が常に上になるようにしたいので上向きのベクトルを[0 1 0]にして使います。
Finally, to come up with a projection matrix, we call XMMatrixPerspectiveFovLH(), with a 90 degree vertical field of view (pi/2), an aspect ratio of 640/480 which is from our back buffer size, and near and far Z at 0.1 and 110, respectively.
最後にプロジェクション行列を用意するためにXMMatrixPerspectiveFovLH()を呼びます。90度の垂直の視界(pi/2)、640/480のアスペクト比(バックバッファのサイズ)、そして近、遠のZ平面をそれぞれと0.1と110にします。
This means that anything closer than 0.1 or further than 110 will not be visible on the screen.
これはスクリーン上の0.1より近いか110より遠い全ての物が見えなくなる事を意味します。
These three matrices are stored in the global variables g_World, g_View, and g_Projection.
これらの3つの行列はグローバル変数 g_World,g_View,g_Projectionに格納されます。
定数バッファの更新
Updating Constant BuffersWe have the matrices, and now we must write them to the constant buffer when rendering so that the GPU can read them.
我々は行列を手に入れましたが、今度は描画時にGPUがそれらを読めるようにするために、それらを定数バッファに書き込まなくてはなりません。
To update the buffer, we can use the ID3D11DeviceContext::UpdateSubresource() API and pass it a pointer to the matrices stored in the same order as the shader's constant buffer.
バッファの更新にはID3D11DeviceContext::UpdateSubresource() APIが使えます。そしてそれに行列が格納されたポインタを渡します。そのポインタの行列が格納されている順番は、シェーダーの定数バッファの並び方と同じです。
To help do this, we will create a structure that has the same layout as the constant buffer in the shader.
これを行うのを助けるために、我々は構造体を作ります。この構造体がシェーダ内の定数バッファと同じレイアウトを持つのです。
Also, because matrices are arranged differently in memory in C++ and HLSL, we must transpose the matrices before updating them.
C++とHLSLの行列は違ったアレンジがなされているので、更新を行う前にそれをトランスポーズ(変換)する必要があります。
//
// 変数の更新
//
ConstantBuffer cb;
cb.mWorld = XMMatrixTranspose( g_World );
cb.mView = XMMatrixTranspose( g_View );
cb.mProjection = XMMatrixTranspose( g_Projection );
g_pImmediateContext->UpdateSubresource( g_pConstantBuffer, 0, NULL, &cb, 0, 0 );
以下訳注:
構造体ConstantBufferはプログラム冒頭の構造体SimpleVertexの後に次の様に宣言されています。
struct ConstantBuffer
{
XMMATRIX mWorld;
XMMATRIX mView;
XMMATRIX mProjection;
};
また、定数バッファを使うためには、パイプラインのステージに登録するために次の関数も呼ぶ必要があります。
ID3D11DeviceContext::VSSetConstantBuffers()
この関数はTutorial04.cpp中ではRender()という関数の中で以下の様に書かれています。
//
// Renders a triangle
//
g_pImmediateContext->VSSetShader( g_pVertexShader, NULL, 0 );
g_pImmediateContext->VSSetConstantBuffers( 0, 1, &g_pConstantBuffer );//これ
g_pImmediateContext->PSSetShader( g_pPixelShader, NULL, 0 );
g_pImmediateContext->DrawIndexed( 36, 0, 0 ); // 36 vertices needed for 12 triangles in a triangle list
ところで・・・Render() という関数は、チュートリアル中で持続的に呼び出し続けてアニメーション描画も行える様に定義されている訳ですが・・・今回の場合、上に挙げた4つの関数の内、本当にここに必要なのは最後の描画関数だけです。
g_pImmediateContext->DrawIndexed( 36, 0, 0 );
これ以外の○SSetなんちゃらかんちゃらみたいな関数は、一旦設定すれば持続します。だから何度も呼ばれるRender()関数内で書かなくても大丈夫です。
例えばチュートリアル中で初期化を行なっている
HRESULT InitDevice(){
・・・
}
という関数の末尾あたりに移動してもOKです。


0 件のコメント:
コメントを投稿